Abstract In Zoroastrianism, Asha represents truth, order, and the cosmic law that upholds reality—a principle that contrasts with the apparent randomness of quantum collapse. This paper proposes that Asha could conceptually eliminate wavefunction collapse in quantum mechanics, preserving superposition as a unified, ordered state. Drawing from interpretations like decoherence and unitary evolution, we introduce a symbolic equation where Asha governs quantum dynamics, offering a philosophical bridge between ancient wisdom and modern physics.
Introduction Quantum mechanics defies classical intuition with its probabilistic core, epitomized by the collapse of the wavefunction—a mysterious process wherein a system in superposition resolves into a definite state upon measurement (Dirac, 1958). Despite its predictive power, the mechanism and necessity of collapse remain debated. In contrast, Zoroastrianism’s Asha—the principle of truth, order, and harmony—suggests a cosmos governed not by randomness, but by coherence (Boyce, 1979). This paper explores whether Asha, as a metaphysical operator, might inspire a collapse-free framework for quantum theory.
Asha in Zoroastrianism Asha (Avestan: aša) is the foundational principle of Zoroastrian cosmology, embodying the intrinsic order of both the moral and material realms. It is the active law of Ahura Mazda, standing in direct opposition to Druj (falsehood and disorder). Asha is not static law but dynamic harmony—a universal resonance through which reality coheres (Dhalla, 1938). While ancient in origin, this metaphysical ideal finds surprising resonance in modern physics’ pursuit of unified, deterministic frameworks.
Quantum Collapse and Its Alternatives In the standard Copenhagen interpretation, a system in a superposition state,
|ψ⟩ = ∑ᵢ cᵢ |i⟩,
collapses upon measurement into a single basis state |i⟩ with probability |cᵢ|² (von Neumann, 1955). However, several interpretations challenge this model:
- Many Worlds Interpretation (MWI): The wavefunction never collapses; all outcomes manifest in branching universes (Everett, 1957).
- Decoherence: Environmental entanglement suppresses interference, mimicking collapse without requiring it (Zurek, 2003).
- Bohmian Mechanics: A guiding wave directs particle behavior, avoiding collapse altogether (Bohm, 1952).
These alternatives suggest that collapse may be epistemic, not ontological—a perspective aligned with Asha’s rejection of arbitrary disorder.
Asha as a Quantum Principle To model Asha’s role in eliminating collapse, we treat it as an operator preserving total coherence. Consider a system S interacting with its environment E:
|ψ_S⟩ |E₀⟩ → ∑ᵢ cᵢ |i_S⟩ |Eᵢ⟩
Rather than collapsing, the entangled state remains unified. We propose a modified Hamiltonian incorporating an “Asha term”:
H = H₀ + H_A,
where H₀ is the conventional system Hamiltonian, and
H_A = λ ∑_{i,j adjacent} |i⟩⟨j|
is an operator coupling adjacent basis states, with λ as a tunable coherence strength. The evolution becomes:
A |ψ⟩ = exp[-i (H₀ + λ ∑_{i,j adjacent} |i⟩⟨j|) t / ℏ] |ψ⟩
This unitary evolution ensures the full wavefunction remains intact, echoing Asha’s metaphysical role in sustaining cosmic harmony.
Breaking Down the Equation Left Side: A |ψ⟩
- A is the Asha operator, symbolizing Zoroastrian order.
- |ψ⟩ is the system’s quantum state, in superposition (|ψ⟩ = ∑ᵢ cᵢ |i⟩).
- A |ψ⟩ represents Asha acting to preserve coherence.
Right Side: exp[-i (H₀ + λ ∑_{i,j adjacent} |i⟩⟨j|) t / ℏ] |ψ⟩
- This is the Schrödinger-style time-evolution of the system.
- H₀ is the standard Hamiltonian (e.g., kinetic + potential energy).
- H_A couples adjacent basis states, sustaining unity.
- λ tunes the strength of this coherence.
- ℏ is the reduced Planck constant.
The total evolution avoids collapse by spreading coherence, mathematically mirroring Asha’s universal order.
Interpretation and Implications This approach aligns with decoherence theory, wherein environmental entanglement explains classicality without invoking true collapse (Schlosshauer, 2007). The speculative H_A term represents non-local coherence, paralleling Bohm’s quantum potential (Bohm & Hiley, 1993). However, unlike the Many Worlds Interpretation, this model retains a single, coherent reality—one sustained by Asha’s principle of unified truth.
Experimentally, this model is indistinguishable from standard quantum predictions, as decoherence already accounts for observed outcomes. However, philosophically, it reframes quantum ontology: instead of collapse as a fundamental event, we interpret it as a perspective-limited illusion. Asha, as a principle of cosmic unity, preserves the integrity of superposition.
Discussion Although the proposed model lacks empirical novelty, it offers a compelling metaphysical synthesis. The Asha-operator framework encourages rethinking quantum randomness as emergent from partial observation rather than ontological chaos. Zoroastrian texts like the Gathas (Insler, 1975) do not address quantum concepts, but their moral and cosmological vision harmonizes with a deterministic, collapse-free universe.
Conclusion This paper introduces a speculative yet conceptually coherent model where Asha eliminates the need for wavefunction collapse by enforcing holistic, unitary evolution. The symbolic equation:
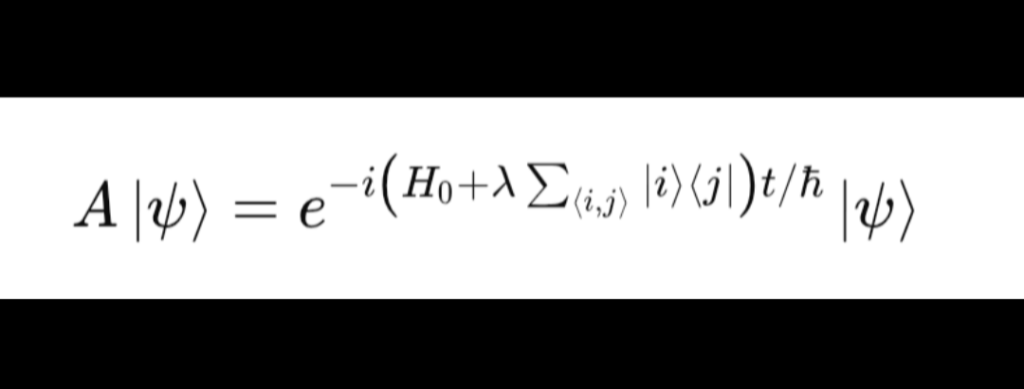
frames Asha as an operator of universal order. While not an empirical theory, this synthesis bridges ancient metaphysical principles and modern quantum mechanics, inviting deeper inquiry into the philosophical dimensions of physical law.
References Bohm, D. (1952). A Suggested Interpretation of the Quantum Theory in Terms of “Hidden” Variables. Physical Review, 85(2), 166–193. Bohm, D., & Hiley, B. J. (1993). The Undivided Universe: An Ontological Interpretation of Quantum Theory. Routledge. Boyce, M. (1979). Zoroastrians: Their Religious Beliefs and Practices. Routledge. Dhalla, M. N. (1938). History of Zoroastrianism. Oxford University Press. Dirac, P. A. M. (1958). The Principles of Quantum Mechanics. Oxford University Press. Everett, H. (1957). “Relative State” Formulation of Quantum Mechanics. Reviews of Modern Physics, 29(3), 454–462. Insler, S. (1975). The Gathas of Zarathustra. Brill. Schlosshauer, M. (2007). Decoherence and the Quantum-to-Classical Transition. Springer. von Neumann, J. (1955). Mathematical Foundations of Quantum Mechanics. Princeton University Press. Zurek, W. H. (2003). Decoherence, Einselection, and the Quantum Origins of the Classical. Reviews of Modern Physics, 75(3), 715–775.
